 代数
代数 【代数】クロネッカー積の定義と計算例
行列\(A = (a_{ij}) \)および行列\(B\)のクロネッカー積は\begin{align}A \otimes B=\begin{pmatrix}a_{11} B & \cdots & a_{1n} B\\a_{21} B & \...
 代数
代数  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学 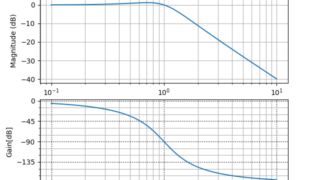 python
python 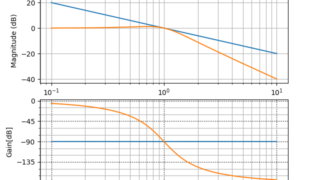 python
python  数学
数学  数学
数学  数学
数学  python
python  python
python  数学
数学 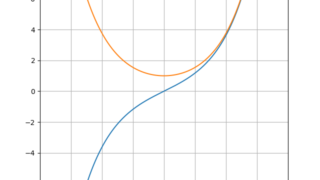 数学
数学  数学
数学 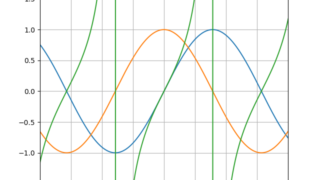 python
python 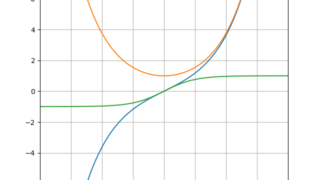 python
python 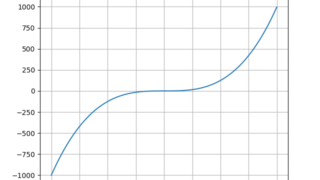 MATLAB/simulink
MATLAB/simulink 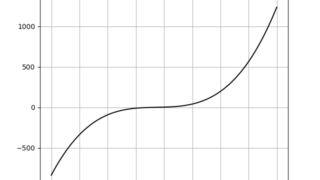 python
python  代数
代数  代数
代数