 数学
数学 【解析】複素数の定義
二次方程式の解の公式\begin{align}x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}\end{align}の判別式\begin{align}D=b^2-4ac\end{align}が負になるとき実数の範囲では解...
 数学
数学  数学
数学  数学
数学 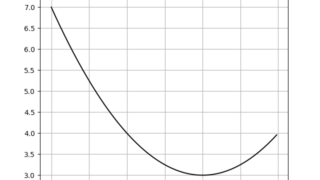 python
python  数学
数学  数学
数学  数学
数学  代数
代数 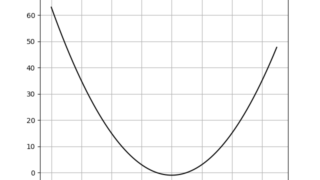 数学
数学