二次関数
\begin{align}
y=ax^2+bx+c \hspace{5mm} (a \neq 0)
\end{align}
のグラフは
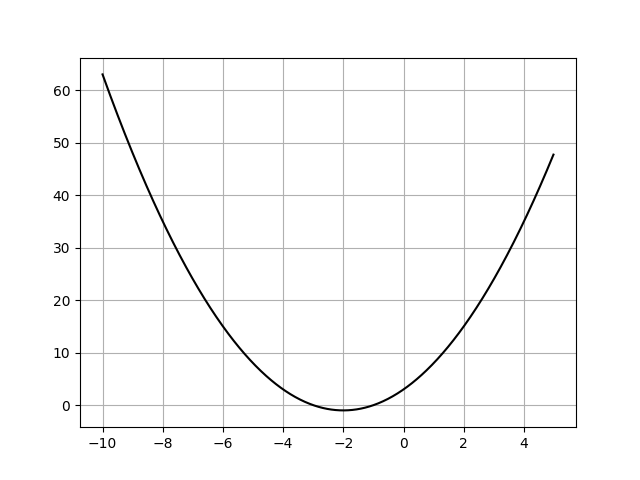
のような形になる。二次関数のグラフとx軸との交点を共有点といい、上図の例ではx軸との共有点の数は2つとなる。
二次関数の共有点の数は二次方程式の解の公式
\begin{align}
x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}
\end{align}
より次のように与えられる。
\(D=b^2-4ac\)とすると共有点の数は
\begin{align}
D>0 & \cdots 2 (異なる二つの実数解)\\
D=0 & \cdots 1 (一つの実数解)\\
D<0 & \cdots 0 (異なる二つの複素解)
\end{align}
となる。



コメント