点Pが楕円の内側にあるかどうか判定する　例１　

点\(P=(2,1)\)が

\begin{align}
\frac{x^2}{2}+\frac{y^2}{4}=1
\end{align}

にあるか調べる。まずGRAPES でグラフを確認する。グラフは

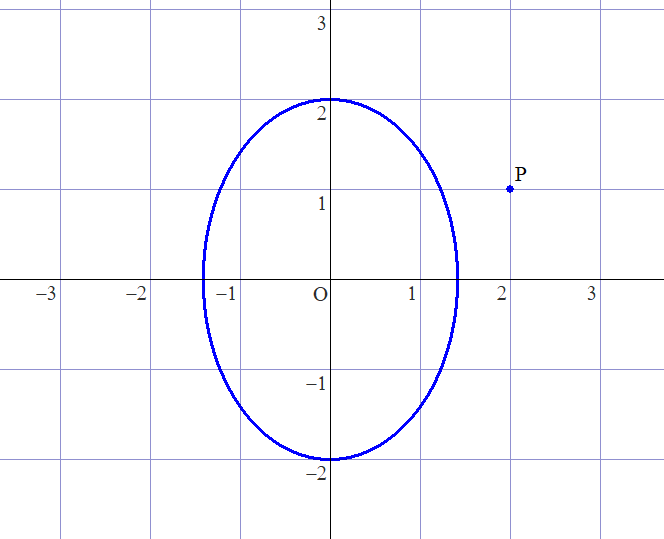
となり、明らかに外に存在する。

まず\(f(x,y)=\displaystyle \frac{x^2}{2}+\frac{y^2}{4}-1\)と置き、\(f(x,y)=0\)を考える。

与式は原点を中心とする楕円であるので原点は楕円の内部に存在する。

\(f(0,0)=-1\)より内部で\(f(x,y)<0\)、外部で\(f(x,y)>0\)である。

ここで\(f(2,1)\)を考えれば

\begin{align}
f(2,1)=2+\frac{1}{4}-1=1.25
\end{align}

上記の条件より楕円の外部に存在する。