 ディジタル制御
ディジタル制御 伝達関数とパルス伝達関数の相互変換について
\(s\)平面から\(z\)平面への変換式は\begin{align}\label{S-T transform}z=e^{sT}\end{align}で与えられる.\(z\)平面上の点および\(s\)平面上の点を\begin{align}z...
 ディジタル制御
ディジタル制御  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学 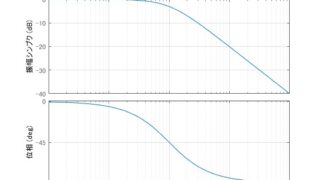 MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学  ディジタル制御
ディジタル制御  ディジタル制御
ディジタル制御  ディジタル制御
ディジタル制御  python
python 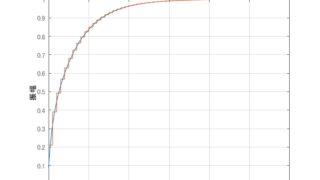 MATLAB/simulink
MATLAB/simulink  ディジタル制御
ディジタル制御