 MATLAB/simulink
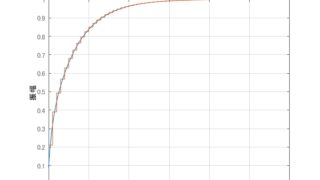
MATLAB/simulink MatlabでPID制御のシミュレーションをする
MatlabでPID制御のシミュレーションをする。システムとPID制御器の伝達関数は\begin{align}P&=\frac{1}{s+1} \\C&=K_P + \frac{K_I}{s} + K_D s \end{align}またフィ...
 MATLAB/simulink
MATLAB/simulink  ロバスト制御
ロバスト制御  python
python  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  python
python  python
python  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  ロバスト制御
ロバスト制御  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学