加法的不確かさは
\begin{align}
\tilde{P}=\{P+\Delta W_a: \|P\|_\infty \leq 1\}
\end{align}
で与えられる。この定義に従い、次のような場合のモデル集合\(\tilde{P}\)を考える。
\begin{align}
P=\frac{\omega^2}{s^2+2 \zeta \omega s+\omega^2} \hspace{5mm} W_{a}=\frac{2s}{s+5}
\end{align}
ノミナルモデル\(P\)は二次遅れ系で、パラメータ\(\omega,\zeta\)は共に\(0.5\)とした。
実行結果は次のとおりである。
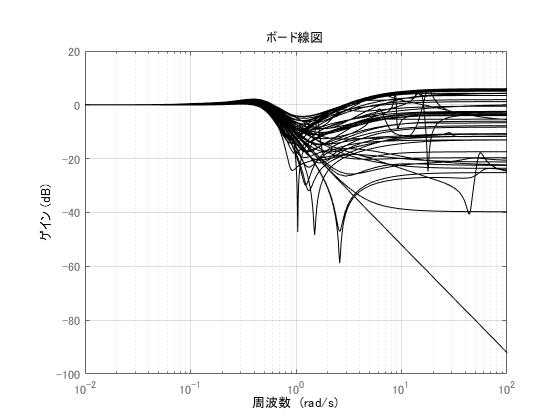
以下ソース
s=tf('s');
omega=0.5;
zeta=0.5;
Pn=omega^2/(s^2+2*zeta*omega*s+omega^2);
Wa=2*s/(s+5);
delta=ultidyn('delta',[1 1],'SampleStateDim',4);
P=Pn+Wa*delta;
P=usample(P,50);
w=logspace(-2,2,100);
figure
bodemag(P,'k')
hold on
bodemag(Pn,w,'k')
grid on




コメント