2つのシステム
\begin{align} G_1=\frac{1}{s} \hspace{10mm} G_2=\frac{1}{s^2+s+1} \end{align}
が直列に接続されているとき、全体のボード線図はそれぞれの伝達関数のボード線図の和になる。
プログラムでの確認結果
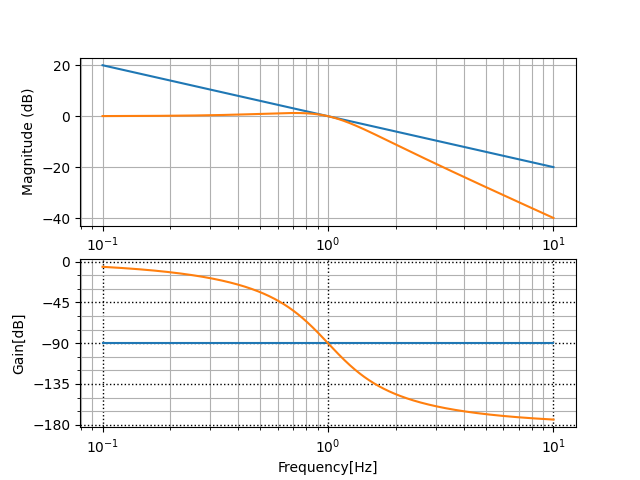
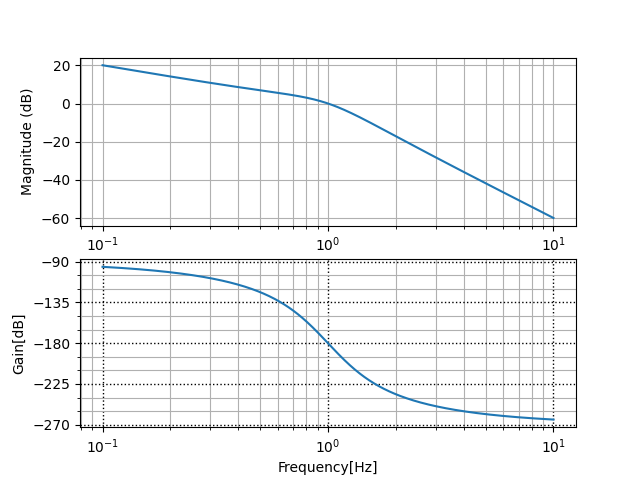
和になっていることが確認できる。
以下コード
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | from control.matlab import *from matplotlib import pyplot as plts = tf('s')G1 = 1 / sG2 = 1 / (s ** 2 + s + 1)plt.figure(1)bode(G1)bode(G2)plt.ylabel("Gain[dB]")plt.xlabel("Frequency[Hz]")plt.grid(color='k', linestyle='dotted', linewidth=1)plt.show()plt.figure(2)bode(G1 * G2)plt.ylabel("Gain[dB]")plt.xlabel("Frequency[Hz]")plt.grid(color='k', linestyle='dotted', linewidth=1)plt.show() |


コメント