 数学
数学 【解析】三角関数の性質1
直角三角形\(ABC\)において、三角関数の定義より次が成り立っている。\begin{align}\sin \theta =\frac{a}{c} \hspace{10mm} \cos \theta =\frac{b}{c}\end{ali...
 数学
数学 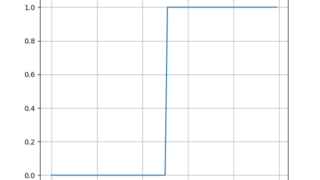 python
python  python
python  制御工学
制御工学  代数
代数  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学 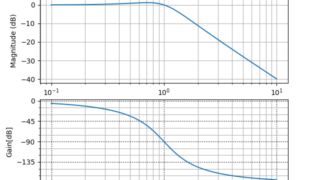 python
python 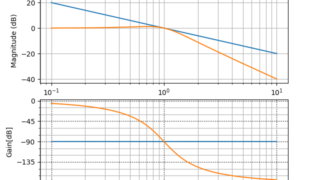 python
python  数学
数学  数学
数学  数学
数学  python
python  python
python  数学
数学 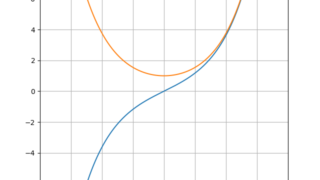 数学
数学  数学
数学  python
python  python
python