 MATLAB/simulink
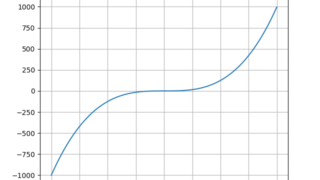
MATLAB/simulink 【解数】Pythonで指数と対数のグラフを描く
指数と対数のグラフを描く。以下ソースコードimport numpy as npimport matplotlib.pyplot as pltx = np.arange(-10.0, 10.0, 0.02)plt.plot(x, x**3)p...
 MATLAB/simulink
MATLAB/simulink 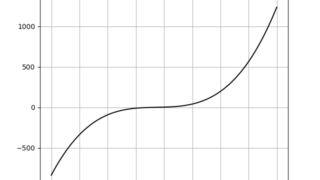 python
python  代数
代数  代数
代数  数学
数学  数学
数学  数学
数学  python
python  数学
数学  数学
数学  数学
数学  代数
代数  数学
数学  数学
数学  数学
数学  代数
代数  数学
数学  代数
代数  代数
代数  python
python