 python
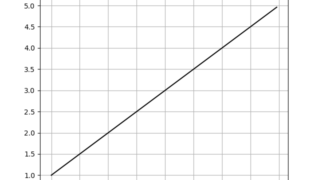
python 【解析】Pythonで一次関数のグラフを描く
pythonで一次関数のグラフを描く。一次関数は\begin{align}f(x)=ax+b (a \neq 0)\end{align}のような関数でこれをただ計算すればいい。例えば\begin{align}y=x+3 \end{align...
 python
python  数学
数学 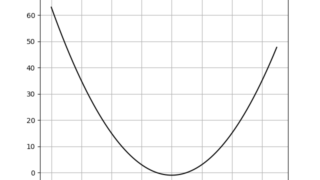 python
python  python
python  python
python  python
python  python
python  python
python  python
python  python
python  python
python  python
python  代数
代数  代数
代数  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink 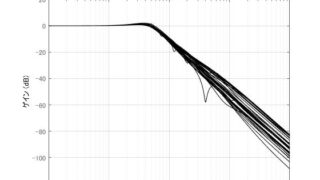 MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  ロバスト制御
ロバスト制御  MATLAB/simulink
MATLAB/simulink