 数学
数学 積分の公式1
\(x^a(a\neq -1)\)の積分\begin{align}\int x^a dx\end{align}は、微分して\(x^a\)となる関数が\(\dfrac{1}{a+1}x^{a+1}\)であるから\begin{align}\in...
 数学
数学  数学
数学 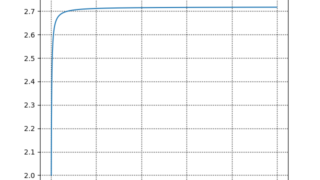 python
python  数学
数学 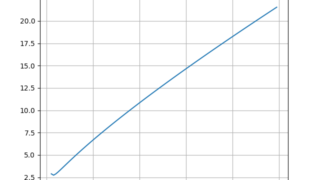 python
python  代数
代数  幾何
幾何  数学
数学  数学
数学  数学
数学 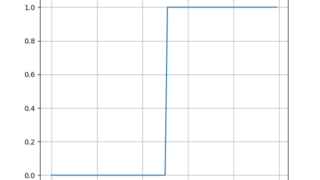 python
python  python
python  代数
代数  数学
数学  数学
数学  数学
数学  python
python  python
python  数学
数学 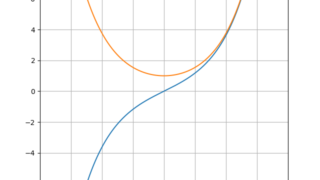 数学
数学