 数学
数学 数列の極限
実数列\(\{a_n|n=0,1,\cdots\}\)において、任意の\(\varepsilon>0\)に対し\(n\ge N\)となる正の整数\(N\)が存在して\begin{align}|a_n-a|<\varepsilon\end{a...
 数学
数学  数学
数学 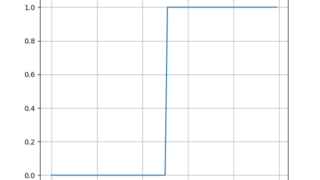 python
python  python
python  数学
数学  数学
数学  数学
数学  python
python  python
python  数学
数学 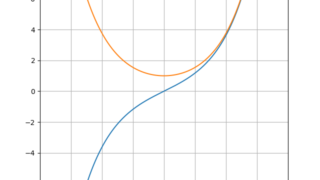 数学
数学  数学
数学 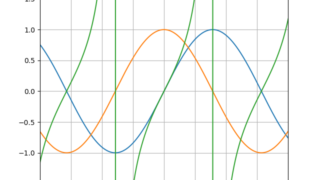 python
python 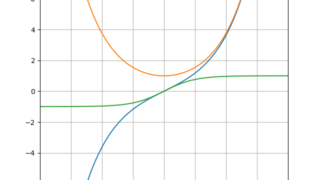 python
python 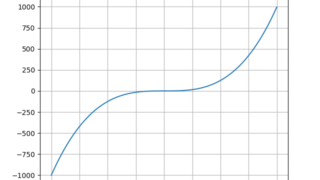 MATLAB/simulink
MATLAB/simulink 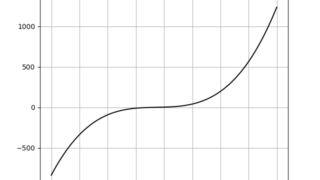 python
python  数学
数学  数学
数学  数学
数学 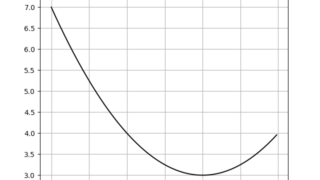 python
python