 数学
数学 【解析】二次関数の頂点の座標
二次関数\begin{align}y=ax^2+bx+c \hspace{5mm} (a \neq 0)\end{align}の頂点の座標について考える。頂点の座標が\((p,q)\)のとき、これを満たす式は\begin{align}y=a...
 数学
数学  数学
数学  数学
数学 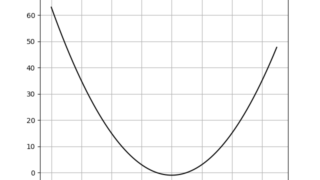 数学
数学  数学
数学  数学
数学  python
python  数学
数学  python
python  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  数学
数学  数学
数学  数学
数学  数学
数学  数学
数学