 MATLAB/simulink
MATLAB/simulink MATLABでフィボナッチ数列を計算する
詳しくは→【C言語】フィボナッチ数列を計算するMATLABでフィボナッチ数列を計算する。以下コード。N=10;F=zeros(1,N+2);n=0;F(1,n+1)=0;n=1;F(1,n+1)=1;for n=0:1:N F(1,n+3)...
 MATLAB/simulink
MATLAB/simulink  python
python 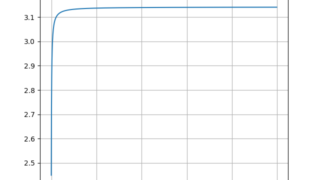 python
python  数学
数学  数学
数学  数学
数学  数学
数学  数学
数学  数学
数学  数学
数学 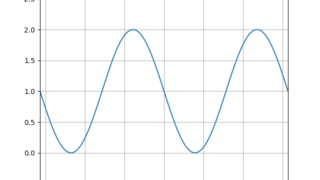 python
python 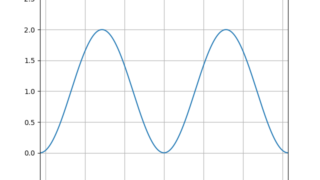 python
python  数学
数学  数学
数学  数学
数学  数学
数学  数学
数学  数学
数学 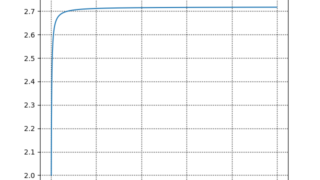 python
python  数学
数学