 数学
数学 【解析】双曲線関数を定義する
双曲線関数はネイピア数\(e\)を用いて\begin{align}\sinh x= \frac{e^{x}-e^{-x}}{2}\\\cosh x= \frac{e^{x}+e^{-x}}{2}\end{align}\(\tanh x\)に...
 数学
数学 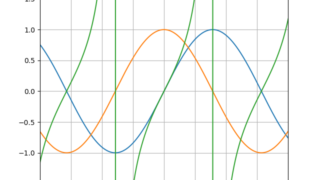 python
python 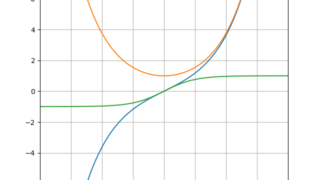 python
python 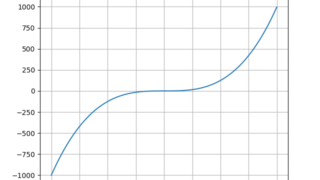 MATLAB/simulink
MATLAB/simulink 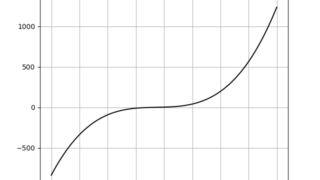 python
python  代数
代数  代数
代数  数学
数学  数学
数学  数学
数学 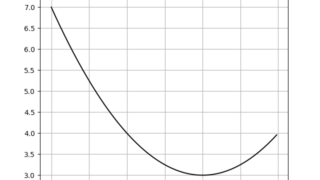 python
python  数学
数学  数学
数学  数学
数学  代数
代数 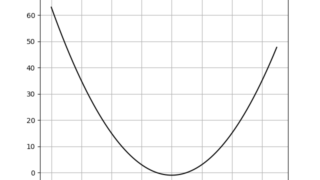 数学
数学  数学
数学  数学
数学  代数
代数  数学
数学