 交流
交流 実効値を導出する
電圧もしくは電流の瞬時式\begin{align}f \left( t \right) = f_m \sin \omega t\end{align}から実効値を求める。二乗平均平方根\begin{align}f_{rms} &= \sqrt...
 交流
交流 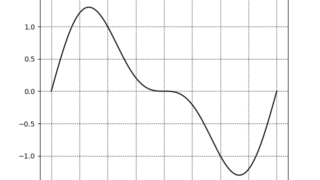 交流
交流 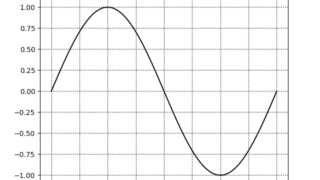 交流
交流  物理
物理  物理
物理  数学
数学  数学
数学  直流
直流  直流
直流  数学
数学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  数学
数学  数学
数学  数学
数学  数学
数学  数学
数学  電気機器
電気機器  電気機器
電気機器