 交流
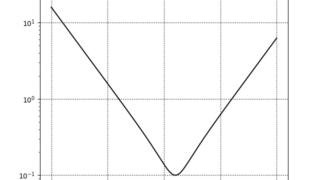
交流 RLC直列回路のインピーダンスの変化
コンデンサのインピーダンスは\(\dot{Z}\)は次式で表される。\begin{align}\dot{Z}=R^2+ j \left ( \omega L - \frac{1}{\omega C} \right )^2\end{align...
 交流
交流  交流
交流  数学
数学  python
python  数学
数学  数学
数学  python
python  数学
数学  python
python  代数
代数  python
python  python
python  数学
数学  数学
数学  python
python  python
python  python
python