グレゴリー・ライプニッツ級数を用いると円周率を計算することができる。グレゴリー・ライプニッツ級数は
\begin{align}
\tan^{-1} x = x – \frac{x^3}{3} + \frac{x^5}{5} + \cdots + \frac{(-1)^{n – 1}x^{2n-1}} {2 n- 1} + \cdots
\end{align}
\(x=1\)のとき
\begin{align}
\frac{x}{4} = 1 – \frac{1}{3} + \frac{1}{5} + \cdots + \frac{(-1)^{n – 1}} {2 n- 1} + \cdots
\end{align}
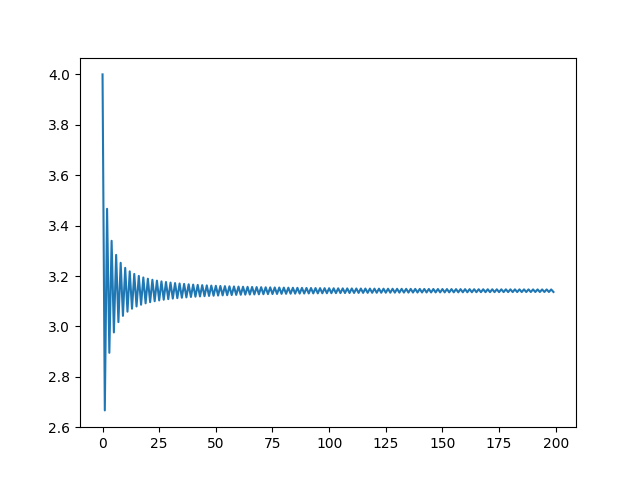
となるので左辺を計算して4倍すれば円周率と等しくなる。収束は遅いので実際に使うにはちょっと微妙。
import numpy as np
from matplotlib import pyplot as plt
n = 200
x = np.zeros(n)
for i in range(n):
x[i] = x[i - 1] + (-1) ** ((i + 1) - 1) / (2 * (i + 1) - 1)
print(4 * x[n - 1])
plt.figure()
plt.plot(4 * x)
plt.show()

コメント