コンデンサのインピーダンスは\(\dot{Z}\)は次式で表される。
\begin{align}
\dot{Z}=R^2+ j \left ( \omega L – \frac{1}{\omega C} \right )^2
\end{align}
これの大きさは
\begin{align}
Z=\sqrt{R^2+ \left ( \omega L – \frac{1}{\omega C} \right )^2}
\end{align}
となるので、周波数を変えてインピーダンスの大きさをプロットすると次のようになる。
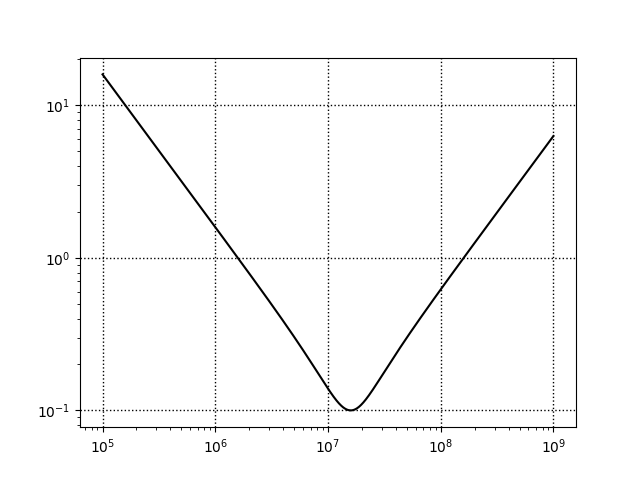
この時の共振周波数は
\begin{align}
f=\frac{1}{2 \pi \sqrt{LC}}
\end{align}
となる。
import numpy as np
from matplotlib import pyplot as plt
R = 0.1
C = 0.1 * 10 ** -6
L = 1 * 10 ** -9
f = np.linspace(100 * 10 ** 3, 1 * 10 ** 9, 10000)
XL = 2 * np.pi * f * L
XC = 1 / (2 * np.pi * f * C)
Z = np.sqrt(R ** 2 + (XL - XC) ** 2)
plt.figure()
plt.plot(f, Z, 'k-')
plt.figure()
plt.plot(f, Z, 'k-')
ax = plt.gca()
ax.set_xscale('log')
ax.set_yscale('log')
plt.grid(color='k', linestyle='dotted', linewidth=1)
plt.show()

コメント