歪波交流はそれぞれの周波数の正弦波の合成で表せるので
\begin{align}
e(t)= \sum_{i=1}^{N} \sqrt{2} E_{i} \sin \left ( \omega_{i} t + \phi_{i} \right )
\end{align}
となる
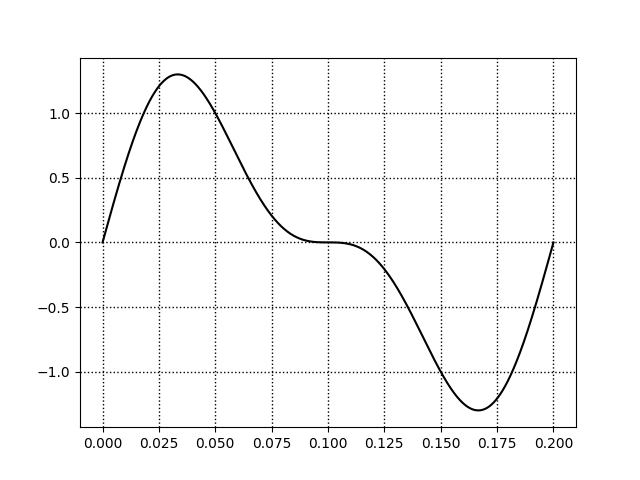
import numpy as np
from matplotlib import pyplot as plt
Em1 = 1
f1 = 5
phi1 = 0
Em2 = 0.5
f2 = 10
phi2 = 0
omega1 = 2 * np.pi * f1
omega2 = 2 * np.pi * f2
t = np.linspace(0, 1 / f1, 1000)
e1 = Em1 * np.sin(omega1 * t + phi1)
e2 = Em2 * np.sin(omega2 * t + phi2)
e = e1 + e2
plt.figure()
plt.plot(t, e, 'k-')
plt.grid(color='k', linestyle='dotted', linewidth=1)
plt.show()

コメント