 制御工学
制御工学 状態方程式と伝達関数の相互変換
線形時不変な状態方程式\begin{align}\dot{x}(t) &= Ax(t)+Bu(t) \\y(t)&=Cx(t)+Du(t)\end{align}と伝達関数との関係について考える。状態方程式をラプラス変換すれば\begin{a...
 制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学 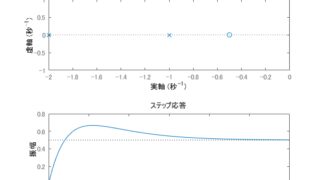 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  ディジタル制御
ディジタル制御  代数
代数  数学
数学  MATLAB/simulink
MATLAB/simulink  Manim
Manim  制御工学
制御工学  解析
解析  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink 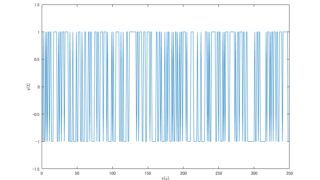 MATLAB/simulink
MATLAB/simulink