 制御工学
制御工学 フィードバック系の伝達関数
今回はフィードバック系の伝達関数を求める。フィードバック系のブロック線図は次のようになる。各信号の関係は\begin{align}E(s)&=R(s)-Y(s)H(s)\\Y(s)&=G(s)E(s)\end{align}で与えられる。初め...
 制御工学
制御工学  物理
物理  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  代数
代数 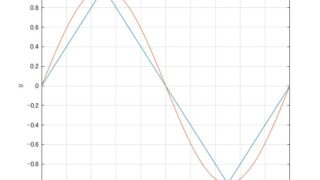 MATLAB/simulink
MATLAB/simulink 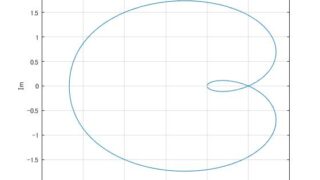 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  代数
代数 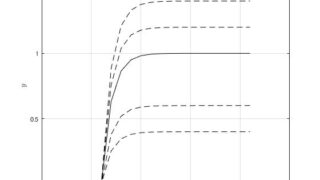 MATLAB/simulink
MATLAB/simulink  英語
英語  MATLAB/simulink
MATLAB/simulink  電気
電気  MATLAB/simulink
MATLAB/simulink  数学
数学  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学