計算機を用いてグラフを描画する際は離散化された値で計算をするためサンプリング周波数は重要である。今回は一例として正弦波について異なるサンプリング周波数で信号の取得を行い、取得波形の確認を行う。
正弦波の式は
\begin{align}
y=\sin \ \omega t
\end{align}
で与えられる。\( \omega\)は角周波数で
\begin{align}
\omega = 2 \pi f
\end{align}
\(f=1\)とした。
サンプリング周波数\(f_{s}\)は\(4 \mathrm{Hz} \)と\(10 \mathrm{Hz} \)で試している。結果はこれ
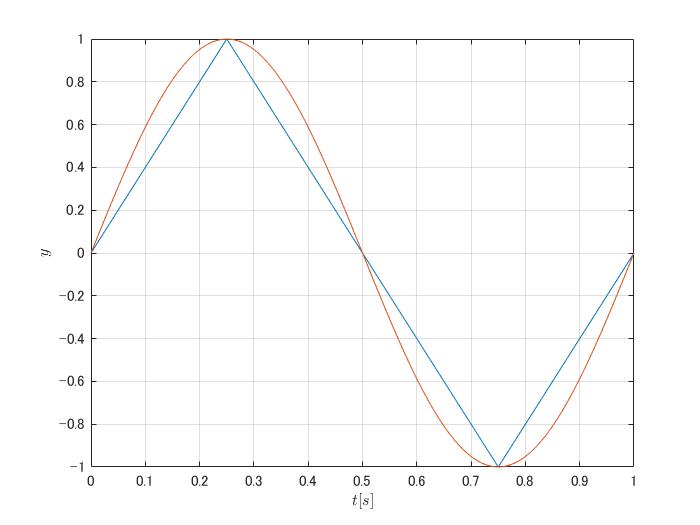
サンプリング周波数が不足すると波形が変わってしまっている。
サンプリング周波数は標本化定理に基づいて決めればいい。標本化定理は
\begin{align}
2 f_{s} \geq f
\end{align}
である。通常は信号の周波数の10倍程度を取っておけば問題ない。
プログラムはこれ。変更すればいろいろ試せる。
f=1;
omega= 2*pi*f;
t=0:0.25:1;
y=sin(omega.*t);
t2=0:0.01:1;
y2=sin(omega.*t2);
figure;
plot(t,y)
hold on
plot(t2,y2)
grid on
xlabel('$t$[$s$]','Interpreter', 'latex');
ylabel('$y$','Interpreter', 'latex');

コメント