 制御工学
制御工学 RLCバンドパスフィルタの伝達関数
回路方程式が\begin{align}E _{I} =L\frac{di}{dt} + \frac{1}{C} \int i dt + Ri\end{align}のようなバンドパスフィルタを考える。いま出力が\begin{align}E_{...
 制御工学
制御工学 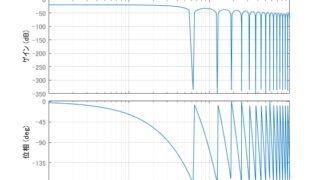 プログラミング
プログラミング  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  ディジタル制御
ディジタル制御  ディジタル制御
ディジタル制御  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学  ディジタル制御
ディジタル制御  制御工学
制御工学  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学 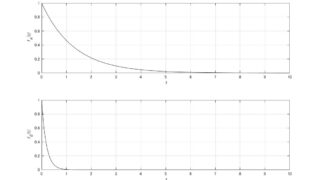 制御工学
制御工学 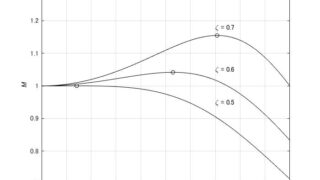 制御工学
制御工学 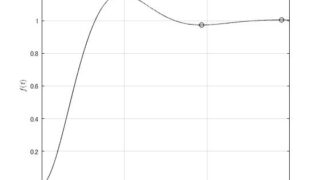 制御工学
制御工学  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink