 制御工学
制御工学 一次遅れシステムの基本形
入力信号\(x(t)\)と出力信号\(y(t)\)の間に次の一階微分方程式が成り立つものを一次遅れ要素もしくは一次要素という。次のような微分方程式を持つシステムは一次遅れ系である。\begin{align}\tau \frac{dy}{dt...
 制御工学
制御工学  制御工学
制御工学  制御工学
制御工学 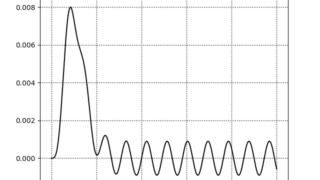 python
python 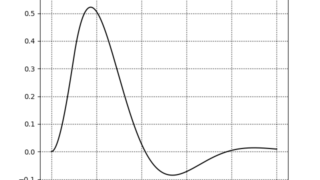 python
python 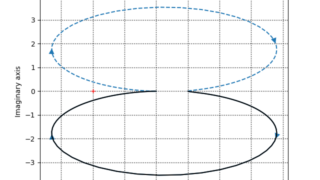 python
python 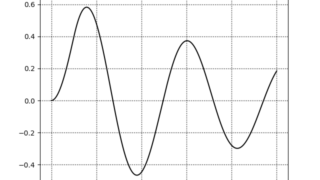 python
python  制御工学
制御工学 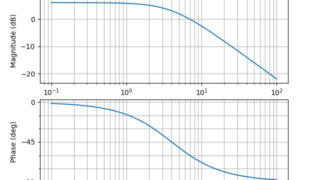 python
python  python
python  制御工学
制御工学 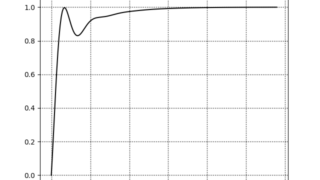 python
python  python
python 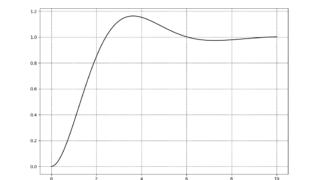 python
python  ディジタル制御
ディジタル制御  システム同定
システム同定 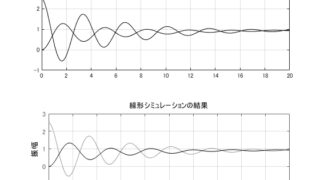 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学