逐次最小二乗法については前回の記事を参照。
逐次最小二乗法を用いて二次遅れ系の伝達関数
\begin{align}
G(s)=\frac{\omega_{n}^2 }{s^2 + 2 \zeta \omega_{n} s + \omega_{n}^2}
\end{align}
をARXモデル
\begin{align}
H(q) = \frac{b_{1} q + b_{2}}{q^{2} + a_{1} q +a_{2}}
\end{align}
に近似する。
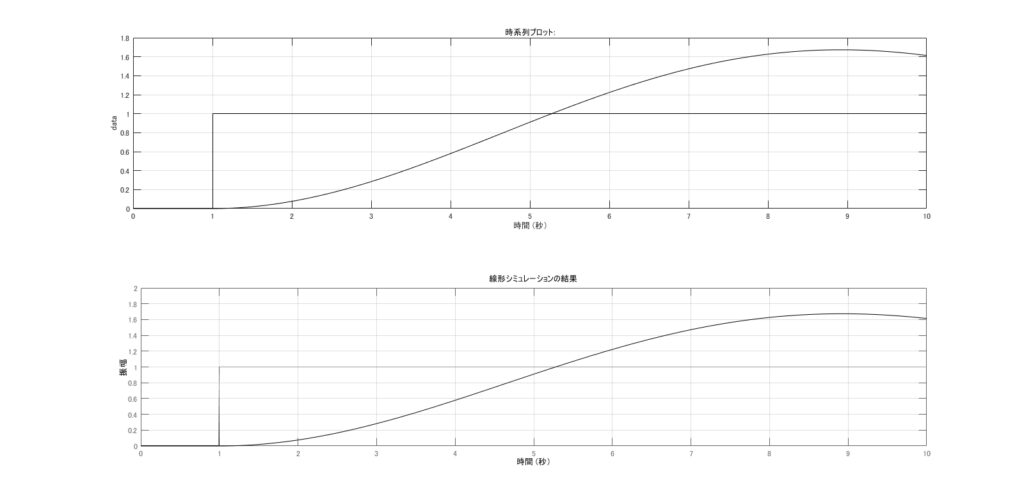
以下プログラム。応答はsimulinkでモデルを作成して取得した。
% 二次遅れ系
Ts=0.01;
s=tf('s');
q=tf('z',Ts);
omega=0.4;
zeta=0.125;
out=sim('test.slx');
y=out.y;
r=out.r;
% ARX model
alpha=1000;
Pn =alpha*eye(4);
est = zeros(length(out.tout),4,1);
Theta=zeros(4,1);
for i=3:1:length(out.tout)
Yn=out.y.data(i);
Zn=[-out.y.data(i-1) -out.y.data(i-2) out.r.data(i-1) out.r.data(i-2)]';
[Theta,Pn] = rls(Theta,Pn,0.95,Yn,Zn);
end
H=(Theta(3)*q+Theta(4))/(q^2+Theta(1)*q+Theta(2));
figure;
subplot(2,1,1)
plot(out.r,'k')
hold on
plot(y,'k');
grid on
subplot(2,1,2)
plot(out.r,'k')
hold on
lsim(H,out.r.data,'k');
grid on


コメント