 制御工学
制御工学 PID制御とは
PID制御とは比例・積分・微分の3つを組み合わせて行う制御方式である。PID制御は次のように与えられる。\begin{align}u(t)=K_P e(t) + K_{I} \int_0^{t} e(\tau) d\tau + K_D \f...
 制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学 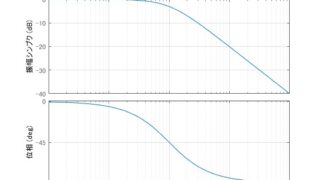 MATLAB/simulink
MATLAB/simulink  python
python 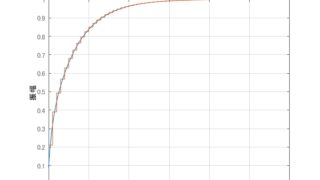 MATLAB/simulink
MATLAB/simulink 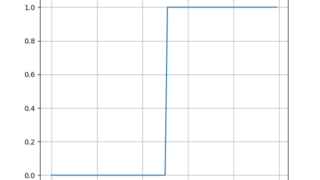 python
python  制御工学
制御工学  制御工学
制御工学 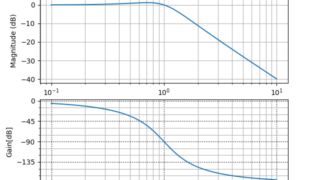 python
python 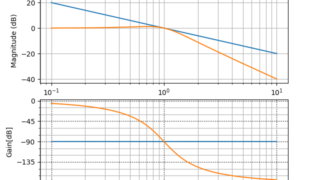 python
python  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学 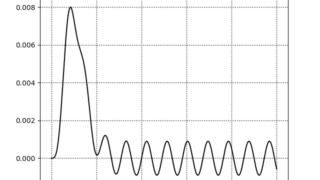 python
python 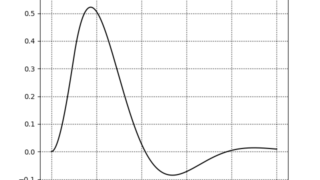 python
python