 python
python Pythonでナイキスト線図を書く
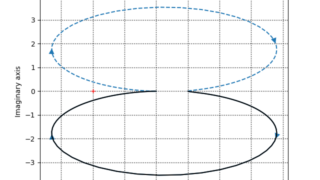
これの続き。Pythonでナイキスト線図を書いてみた。from control.matlab import *import numpy as npfrom matplotlib import pyplot as pltN=100t=np.l...
 python
python  制御工学
制御工学  python
python  python
python  制御工学
制御工学  python
python  python
python  python
python  ディジタル制御
ディジタル制御  システム同定
システム同定  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  ディジタル制御
ディジタル制御  ディジタル制御
ディジタル制御  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学 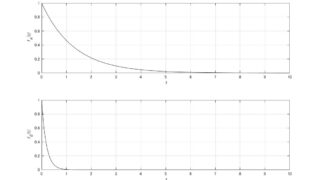 制御工学
制御工学 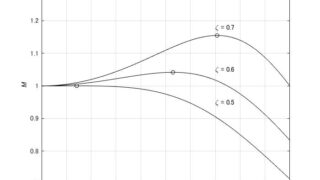 制御工学
制御工学