 制御工学
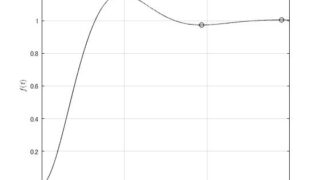
制御工学 二次遅れ系の過渡応答の極大極小値
二次遅れ系の伝達関数\(G(s)\)\begin{align}G(s)=\dfrac{\omega_{n}^2}{s^2 + 2 \zeta \omega_{n} s+ \omega_{n}^2}\end{align}についての行過ぎ量を求...
 制御工学
制御工学  制御工学
制御工学 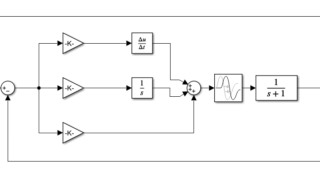 MATLAB/simulink
MATLAB/simulink 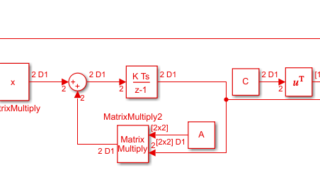 MATLAB/simulink
MATLAB/simulink  古典制御
古典制御  MATLAB/simulink
MATLAB/simulink 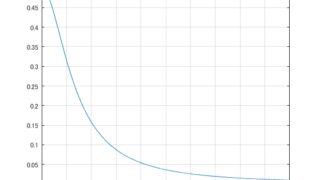 MATLAB/simulink
MATLAB/simulink 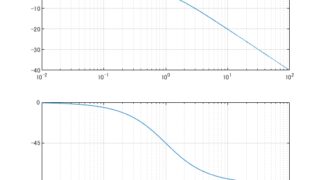 MATLAB/simulink
MATLAB/simulink 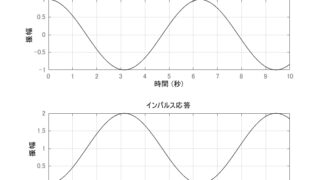 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink 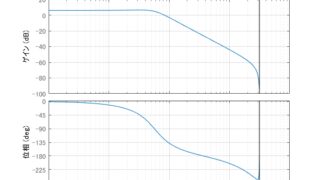 MATLAB/simulink
MATLAB/simulink 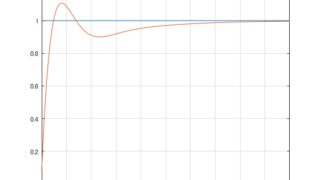 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学 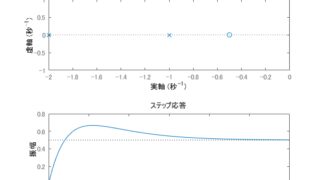 MATLAB/simulink
MATLAB/simulink  ディジタル制御
ディジタル制御  MATLAB/simulink
MATLAB/simulink