 数学
数学 ベクトル関数の定義
ある実数\(t\)によってベクトル\(A\)が定まる時、これをベクトル関数といい\(A(t)\)と書く。\(A(t)\)の変数が\(A_x,A_y,A_z\)であれば\begin{align}A(t)=A_x(t) \boldsymbol{...
 数学
数学  代数
代数  代数
代数  電気
電気  数学
数学  代数
代数  代数
代数  幾何
幾何  英語
英語  代数
代数  幾何
幾何  代数
代数 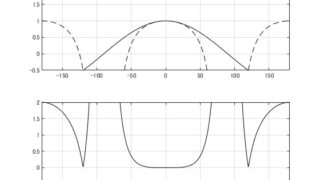 MATLAB/simulink
MATLAB/simulink 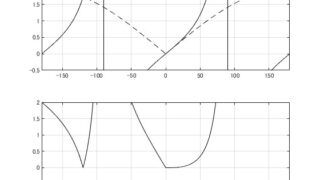 MATLAB/simulink
MATLAB/simulink  物理
物理  物理
物理  数学
数学  数学
数学  数学
数学  英語
英語