 制御工学
制御工学 特性方程式とシステムの安定性
今線形時不変なシステムの伝達関数が\begin{align}G(s)=\frac{N(s)}{D(s)}\end{align}で与えられているとする。このとき、伝達関数の分母から作られる特性方程式\(D(s)=0\)を調べることで安定性を知...
 制御工学
制御工学 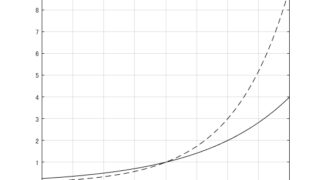 数学
数学  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink 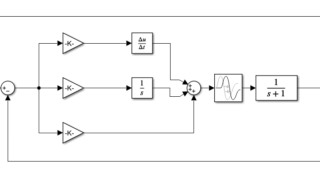 MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  数学
数学  代数
代数  電気機器
電気機器 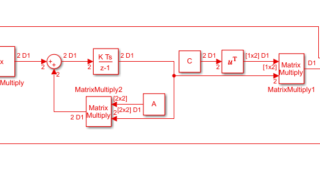 MATLAB/simulink
MATLAB/simulink 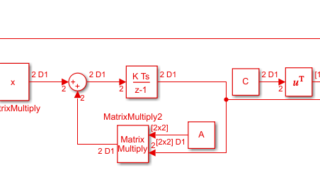 MATLAB/simulink
MATLAB/simulink  古典制御
古典制御  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink 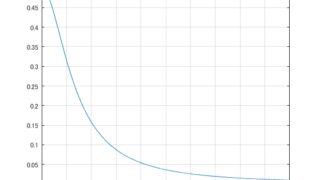 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink 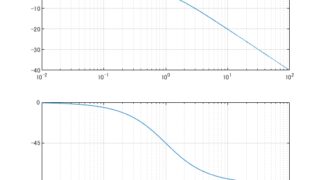 MATLAB/simulink
MATLAB/simulink  制御工学
制御工学 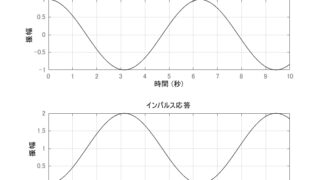 MATLAB/simulink
MATLAB/simulink