 英語
英語 海外で発売されている日本のアニメを使って楽しく英語を勉強する
英語の勉強をするとき有名な参考書はDUOシリーズやロイヤル英文法シリーズなどがあり、ほかにもたくさん出版されています。が、私はちょっと面白くなくてこれらの本では英語力があまり伸びませんでした。もともとアニメをよく見ることもあり、日本のアニメ...
 英語
英語  MATLAB/simulink
MATLAB/simulink  危険物取扱者
危険物取扱者  制御工学
制御工学  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  数学
数学  電気
電気  電子回路
電子回路  電子回路
電子回路  電験
電験  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  物理
物理 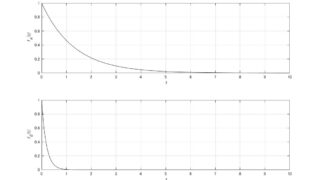 制御工学
制御工学 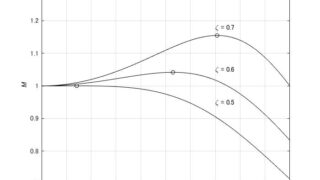 制御工学
制御工学 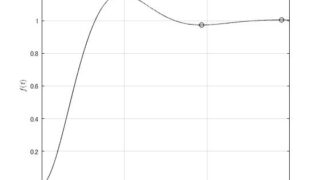 制御工学
制御工学  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#