 制御工学
制御工学 線形時不変システムの可観測性
線形時不変な状態方程式\begin{align}\dot{x}(t) &= Ax(t)+Bu(t) \\y(t)&=Cx(t)+Du(t)\end{align}が不可観測であるとする。不可観測性から求められる異なった二つの初期値を\(x_A...
 制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学 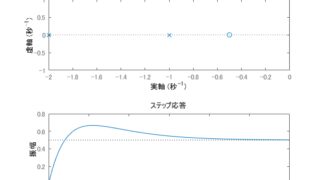 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  ディジタル制御
ディジタル制御  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink