 python
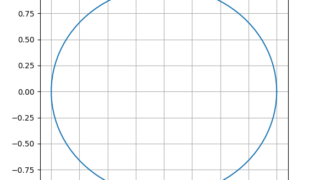
python Pythonでexp(iθ)が円になることを調べる
オイラーの公式によれば\begin{align}e^{i \theta} = \cos \theta + i \sin \theta\end{align}となり、円になる。右辺が円になることは直観的に確認できるが左辺については直観的ではない...
 python
python  python
python  python
python 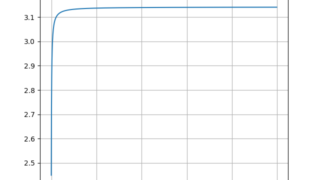 python
python  python
python 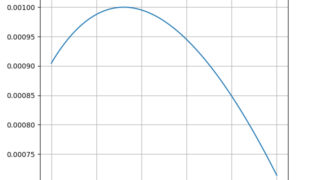 python
python 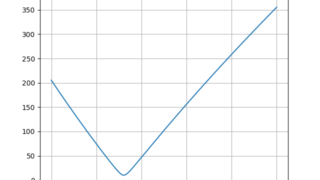 python
python  python
python  python
python  python
python  python
python 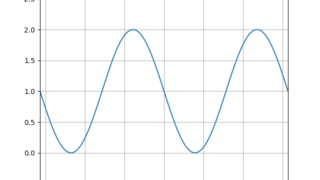 python
python  python
python 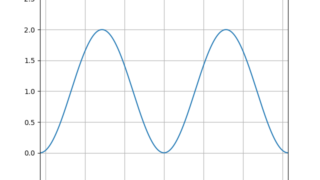 python
python 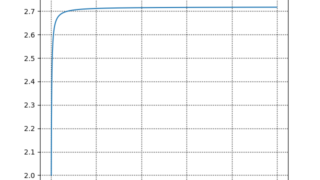 python
python 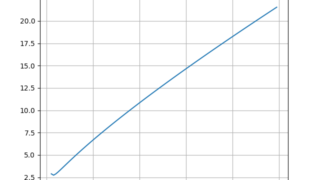 python
python 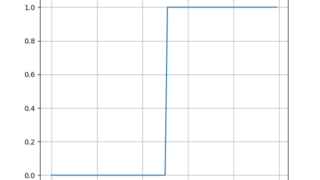 python
python  python
python 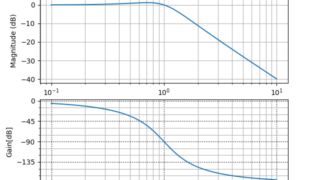 python
python 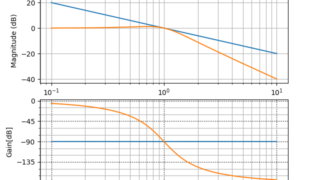 python
python