オイラーの公式によれば
\begin{align}
e^{i \theta} = \cos \theta + i \sin \theta
\end{align}
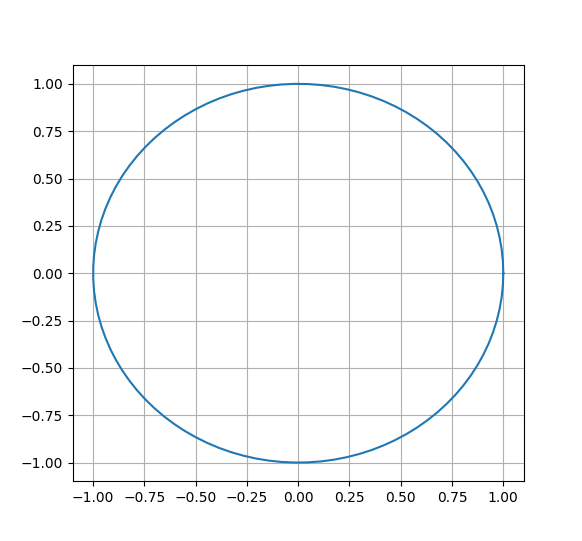
となり、円になる。
右辺が円になることは直観的に確認できるが左辺については直観的ではないのでPythonで確認する。
結果。当たり前だが円になる。
以下コード
import numpy as np
import matplotlib.pyplot as plt
N = 100
theta = np.linspace(0, 2*np.pi, N)
y = [0] * N
yreal = [0] * N
ycomp = [0] * N
count = 0
for angle in theta:
y[count] = np.e**(angle*1j)
yreal[count] = y[count].real
ycomp[count] = y[count].imag
count = count + 1
print(y)
plt.plot(yreal, ycomp)
plt.grid()
plt.show()

コメント