 python
python 次回の番号を予測してみて
予測されたロト7の当選番号: これうまくいってるのかな
 python
python  python
python  python
python  python
python  python
python  python
python  python
python  python
python  python
python  python
python  python
python  python
python  python
python  python
python 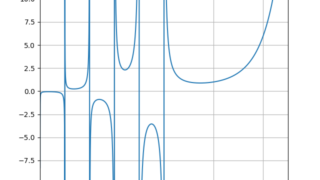 python
python  python
python 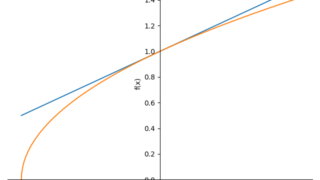 python
python 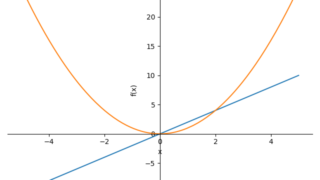 python
python  python
python  python
python