 幾何
幾何 正五角形の対角線の長さ
正五角形の1辺の長さを1とすると正五角形の対角線の長さ\(a\)は余弦定理より\begin{align}a^2&=1^2 + 1^2 - 2 \times 1 \times 1 \times \cos 108\\&= 2 - 2 \time...
 幾何
幾何  幾何
幾何  幾何
幾何 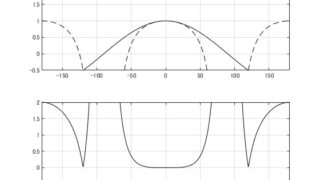 MATLAB/simulink
MATLAB/simulink 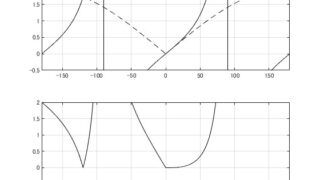 MATLAB/simulink
MATLAB/simulink  C/C++/C#
C/C++/C#  MATLAB/simulink
MATLAB/simulink  幾何
幾何  幾何
幾何  幾何
幾何  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  python
python  幾何
幾何  幾何
幾何  python
python  python
python  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#