 MATLAB/simulink
MATLAB/simulink MATLABでシステム同定用のM系列信号を生成する
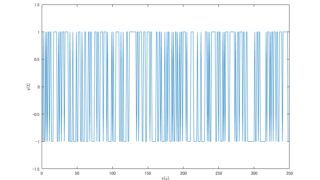
MATLABでシステム同定用のM系列信号を生成する。ツールボックスがないと動かない可能性があるので注意。結果がこんな感じ。コードN = 350;u = idinput(N,'rbs');figureplot(u)ylim()xlabel('...
 MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学