 制御工学
制御工学 線形システムが可安定であるとは
線形システム\begin{align}\dot{x} (t) = A x(t) + B u(t)\end{align}について、行列\begin{align}A-BK\end{align}の固有値の実部が全て負になるような状態フィードバック...
 制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学 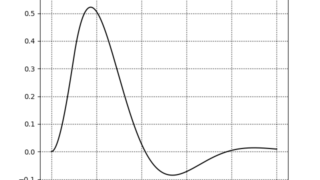 python
python  制御工学
制御工学  制御工学
制御工学  代数
代数 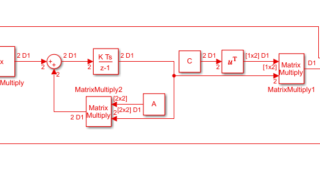 MATLAB/simulink
MATLAB/simulink 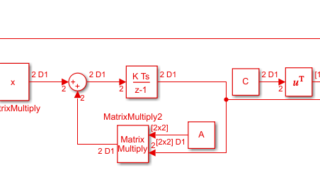 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink 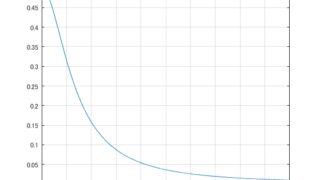 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学