 制御工学
制御工学 状態方程式の同値変換
次の状態方程式で表現されるシステム\begin{align}\dot{x}(t) &=Ax(t)+Bu(t)\\y(t)&=Cx(t)\end{align}において任意の正則な行列\(T¥)を使って\begin{align}\overlin...
 制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学 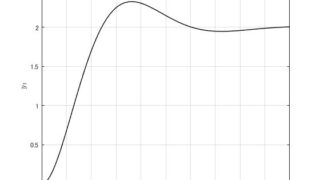 MATLAB/simulink
MATLAB/simulink  制御工学
制御工学