 制御工学
制御工学 ルーリエ系の定義
線形時不変なシステム\begin{align}\dot{x}(t)&=Ax(t) + bu(t)\\y(t)&=cx(t) \\e(t)&=-y(t)\end{align}に対しフィードバック則\begin{align}u(t)=\phi(...
 制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  代数
代数 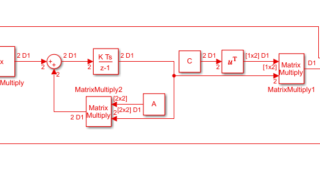 MATLAB/simulink
MATLAB/simulink 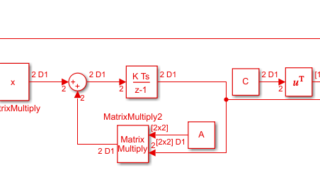 MATLAB/simulink
MATLAB/simulink  古典制御
古典制御  MATLAB/simulink
MATLAB/simulink 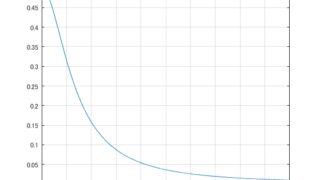 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink 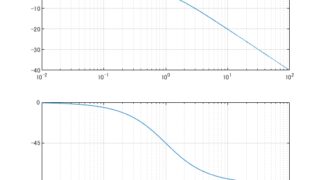 MATLAB/simulink
MATLAB/simulink  制御工学
制御工学 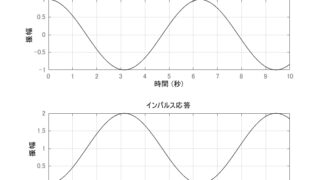 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink 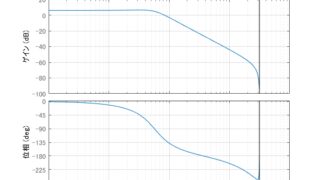 MATLAB/simulink
MATLAB/simulink 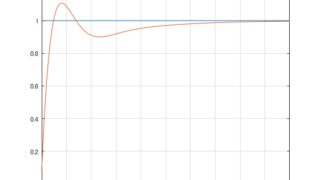 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学