 MATLAB/simulink
MATLAB/simulink ボード線図の示す意味と応答への影響
伝達関数とボード線図の関係を考察する。今伝達関数が\begin{align}G(s)=\frac{s^2+1}{s^2+6s+8}\end{align}で与えられているとする。この時の分子多項式に\(s=-j \omega\)を代入した時明...
 MATLAB/simulink
MATLAB/simulink 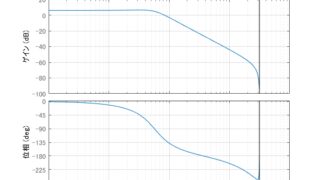 MATLAB/simulink
MATLAB/simulink 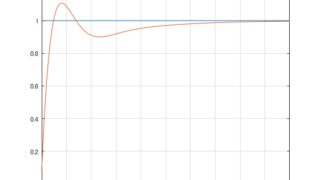 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  C/C++/C#
C/C++/C#  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学