 MATLAB/simulink
MATLAB/simulink MATLABの互換にはGNU Octaveがいいらしい
GNU Octaveを試してみる。フリーなので今ある記事も置き換える予定。
 MATLAB/simulink
MATLAB/simulink 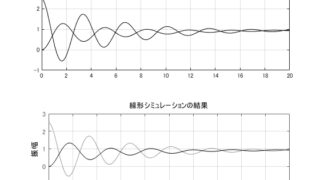 MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  工作
工作  制御工学
制御工学  制御工学
制御工学 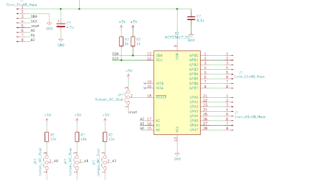 電子回路
電子回路  プログラミング
プログラミング  プログラミング
プログラミング  制御工学
制御工学  電験
電験  C/C++/C#
C/C++/C# 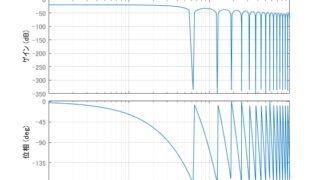 プログラミング
プログラミング  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink  ディジタル制御
ディジタル制御  電験
電験  MATLAB/simulink
MATLAB/simulink