 電気機器
電気機器 需要率と負荷率と不等率
需要率と負荷率と不等率は次のように定義される。\begin{align}需要率=\frac{最大需要電力}{設備容量} \times 100\end{align}\begin{align}負荷率=\frac{平均需要電力}{最大需要電力} ...
 電気機器
電気機器  電力
電力  直流
直流  直流
直流  物理
物理  交流
交流  交流
交流  交流
交流  交流
交流  電気機器
電気機器  交流
交流  交流
交流 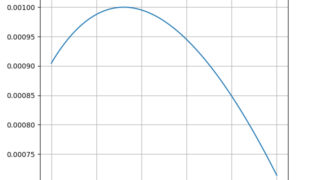 python
python  電力
電力 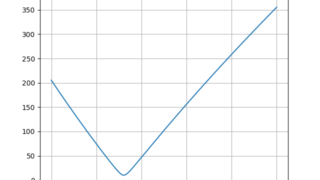 python
python  python
python  python
python  python
python  数学
数学  ディジタル制御
ディジタル制御