 代数
代数 【代数】二次方程式の定義
次のような\begin{align}ax^2+bx+c=0(a \neq 0)\end{align}\(x\)についての最高次数が2である方程式を二次方程式という。注釈中の\(a \neq 0\)がなければ\(a = 0\)となる場合が存在...
 代数
代数  制御工学
制御工学  MATLAB/simulink
MATLAB/simulink 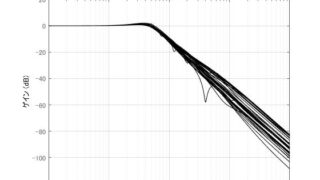 MATLAB/simulink
MATLAB/simulink  制御工学
制御工学  ロバスト制御
ロバスト制御  MATLAB/simulink
MATLAB/simulink  MATLAB/simulink
MATLAB/simulink  制御工学
制御工学