ウォリスの公式と円周率

次の無限積をウォリスの公式という。

\begin{align}
\lim_{m \to \infty} \large \prod_{n=1}^m \frac{4n^2}{4n^2-1}=\frac{\pi}{2}
\end{align}

ウォリスの公式を用いると円周率を計算することができるが、収束はとても遅い。今回はウォリスの公式をプログラミングで実装し円周率を計算してみようと思う。（収束速度がどの程度かは今後調べる。）

コードは以下の通り。

N=100;
x=1:1:N;

w=zeros(1,N);

w(1,1)=4/3;

for i=2:1:N
    w(1,i)=w(1,i-1)*4*x(1,i)^2/(4*x(1,i)^2-1);
end

figure
plot(2.*w)

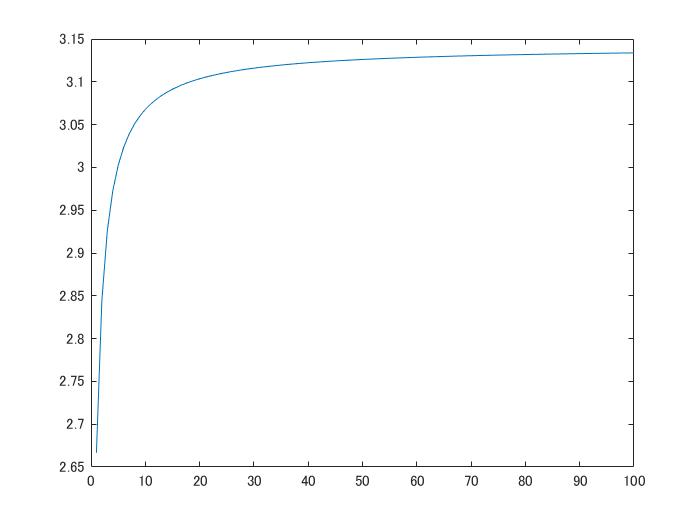
結果を二倍して表示した。\(\pi \)に収束していくグラフが描ける。