ゼータ関数の特殊値を計算する

ゼータ関数
\begin{align}
\zeta(s) = \sum_{n=1}^{\infty} \dfrac{1}{n^s} =\dfrac{1}{1^s}+\dfrac{1}{2^s}+\dfrac{1}{3^s}+\dfrac{1}{4^s} + \cdots
\end{align}
の\(s\)に整数を代入して得られる値をゼータ関数の特殊値あるいはゼータ定数と呼ぶらしい。
今回は以下の\(s=1,2,3\)のゼータ関数の特殊値を計算する。
これらの値はすでに求められており

\(s=1\)の時、ゼータ関数の特殊値は調和級数と呼ばれ
\begin{align}
\zeta(1) = \sum_{n=1}^{\infty} \dfrac{1}{n} = 1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4} + \cdots= \infty
\end{align}
\(s=2\)の時、ゼータ関数の特殊値はバーゼル問題と呼ばれ
\begin{align}
\zeta(2) = \sum_{n=1}^{\infty} \dfrac{1}{n^2} =\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2} + \cdots= \dfrac{\pi^2}{6}
\end{align}
\(s=3\)の時、ゼータ関数の特殊値はアぺリーの定数と呼ばれ
\begin{align}
\zeta(3) = \sum_{n=1}^{\infty} \dfrac{1}{n^3} =\dfrac{1}{1^3}+\dfrac{1}{2^3}+\dfrac{1}{3^3}+\dfrac{1}{4^3} + \cdots= 1.20205 \cdots
\end{align}

ゼータ関数の特殊値は\(n=N\)までの部分和を順に求める。
例えば調和級数において部分和を求めれば

\(N=1\)までの部分和
\begin{align}
\zeta(1) = 1
\end{align}
\(N=2\)までの部分和
\begin{align}
\zeta(1) = 1 + \dfrac{1}{2}
\end{align}
\(N=3\)までの部分和
\begin{align}
\zeta(1) = 1 + \dfrac{1}{2} + \dfrac{1}{3}
\end{align}

これをMATLABで行うためのコードは

n=50;

y1=func(n,1);
y2=func(n,2);
y3=func(n,3);

fig = figure('name', 'ゼータ関数の特殊値');

tunefig('ppt', fig);         % 一枚だけ編集

plot([1:1:n],y1,'k-');
hold on
plot([1:1:n],y2,'k--');
hold on
plot([1:1:n],y3,'k-.');
grid on
legend('s=1(調和級数)','s=2(バーゼル問題)','s=3(アぺリーの定数)');
xlabel('$n$','Interpreter', 'latex');
ylabel('$\zeta(s)$','Interpreter', 'latex');
ylim([0 7])
function y=func(M,s)
    temp=0;
    temp2=zeros(1,M);
    
    for i=1:1:M
        temp= temp + 1 ./ i^s;
        temp2(1,i)=temp;
    end
    y=temp2;
end

結果は

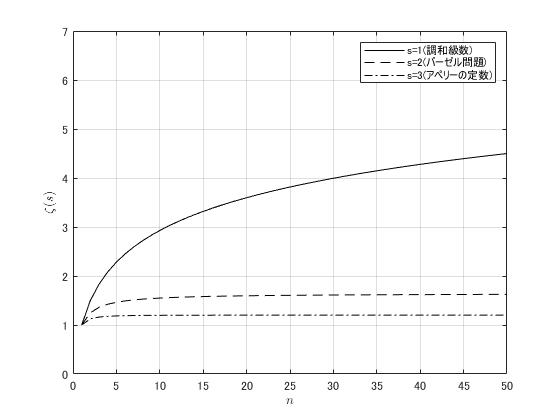
数値計算であるため多少誤差があるが、きちんと理論値に収束してそうだ。

参考文献
MATLABでLaTeX論文用の図を整形する