ブリッジ回路の平衡条件

下図のような回路をブリッジ回路という。

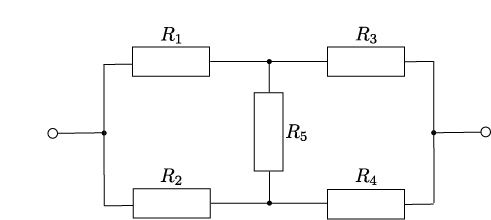
抵抗$R_{5}$に流れる電流$I_{5}$が$0$であるとき、そのブリッジ回路は平衡という。
平行条件を求める。キルヒホッフの法則より
$$\begin{align} E= R_{1} I_{1} + R_{3} I_{1} \hspace{10mm} E= R_{2} I_{2} + R_{4} I_{2} \end{align}$$
電流$I_{1},I_{2}$は
$$\begin{align} I_{1}=\frac{E}{R_{1} + R_{3}} \hspace{10mm} I_{2}=\frac{E}{R_{2} + R_{4}} \end{align}$$
$V_{a},V_{b}$の電位は
$$\begin{align} V_{b}=R_{3} I_{1} = \frac{R_{3}}{R_{1} + R_{3}} E \hspace{10mm} V_{c}=R_{4} I_{2} = \frac{R_{4}}{R_{2} + R_{4}} E \end{align}$$
平衡条件より$V_{b}=V_{c}$が成り立つので
$$\begin{align} \frac{R_{3}}{R_{1} + R_{3}} E = \frac{R_{4}}{R_{2} + R_{4}} E \end{align}$$
より
$$\begin{align} R_{1} R_{4} = R_{2} R_{3} \left [ \mathrm{\Omega} \right ] \end{align}$$
を得る。