 コミケ・展示会等
コミケ・展示会等 コミックマーケット101への参加について
Twitterでは何度か宣伝をしていますがコミックマーケット101へ参加します。曜日と場所は「土曜日 西地区“す”ブロック-14b」です。詳しい場所は以下のURL参照。サークルカットのとおりオーディオアンプを作ったので、アンプ基板と同人誌を...
 コミケ・展示会等
コミケ・展示会等  交流
交流  電子回路
電子回路  電子回路
電子回路  機械
機械  機械
機械  物理
物理  代数
代数  数学
数学 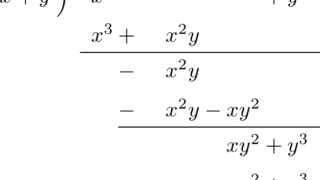 代数
代数  英語
英語  幾何
幾何  C/C++/C#
C/C++/C#  工作
工作  C/C++/C#
C/C++/C#  電子回路
電子回路  C/C++/C#
C/C++/C#  C/C++/C#
C/C++/C#  制御工学
制御工学  C/C++/C#
C/C++/C#